Resources - Financial Terms

Internal Rate of Return, Net Present Value, Discount Rate and Discounted Cash Flow

The Internal Rate of Return (IRR) is the interest rate received for an investment consisting of expenses (negative values) and income (positive values) that occur at regular periods. IRR measures the average annual yield on an investment. For an income-producing property, the IRR calculation uses the initial amount invested in the property, a series of projected after-tax cash flows and a projected after-tax sales proceeds amount in a given year.

To find the IRR, find the value of r that satisfies the following equation:

Net Present Value (NPV) is the sum of all future periodic net cash flows discounted to the beginning period.

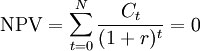
Ct = Cash Flow in month t
r = Internal Rate of Return
N = Total number of periods

This NPV summation equation cannot be solved for IRR analytically but only via iterations. Solving this NPV summation equation for IRR is essentially a matter of computational guesswork. To solve the equation pick values for IRR until the NPV is equal to zero, or very close to zero. The iteration process can be quite time consuming and tedious.

Rather than go through the iterations by hand, using the IRR derived from Excel (view Excel File) of approximately 30.242%, the accuracy of the IRR can be proven as follows. Insert -75,000 for t1, 25,000 for t2 . . . until you have plugged in all the whole numbers from 3 to 10. The result should be 0, or very close to zero. Note: -75000 = -100,000 + 25,000 = the Initial Investment plus the first year cash flow.

IRR Examples

Method using t = 1

NPV = [-75,000/(1 + 0.30242)^1] + 25,000/(1 + 0.30242^2] + [25,000/(1 + 0.30242)^3] + [25,000/(1 + 0.30242)^4] + [25,000/(1 + 0.30242)^5] + [25,000/(1 + 0.30242)^6] + [25000/(1 + 0.30242)^7] + [25000/(1 + 0.30242)^8] + [25000/(1 + 0.30242)^9] + [25000/(1 + 0.30242)^10] = -57,585 + 14,738 + 11,316 + 8,688 + 6,671 + 5,122 + 3,933 + 3,019 + 2,318 = approximately 0

Method using t = 0

NPV = [-100,000/(1 + 0.21406)^0] + [25000/(1 + 0.21406)^1] + [25000/(1 + 0.21406)^2] + [1/(1 + 0.21406)^3] + [1/(1 + 0.21406)^4] + [1/(1 + 0.21406)^5] + [/(1 + 0.21406)^6] + [25000/(1 + 0.21406)^7] + [25000/(1 + 0.21406)^8] + [25000/(1 + 0.21406)^9] + [25000/(1 + 0.21406)^10] = -100,000 + 20,592 + 16,961 + 13,970 + 11,507 + 9478 + 7807 + 6430 + 5297 + 4363 + 3594 = approximately 0

The problem with using period zero in the calculation of NPV is Excel considers period 0 to be of equal length to the other periods. So when Excel determines the IRR, Excel uses 11 periods rather than 10.

Wether or not you choose to use a time period of 0 depends on your preference.

Notes

When verifying the IRR using Excel, it is necessary to add small positive values in periods where cash flow is equal to zero. Otherwise Excel will ignore periods where cash flow is equal to zero.
When using the IRR formula in Excel, it is necessary to divide by the desired number of periods in one year. For example, when finding the IRR using monthly periods, the IRR must be multiplied by 12.
Excel often gives errors for IRR calculations unless a guess amount is entered in the formula dialog box. This guess amount is used by Excel as a starting value for iterations to solve for IRR, and should be a value that is close to the actual IRR.

Net Present Value (NPV)

The NPV, (also known as Net Present Value of Discounted Cash Flows) is the sum of all future periodic net cash flows discounted to the present, using the discount rate. The discount rate reflects the investment risk and anticipated return required to take that risk. The discount rate is the annual return that an investor would expect to receive from an alternative investment or the amount that an investor would like to receive on the investment.

The NPV is used to estimate the attractiveness of real estate investments.

If an investor has two investment opportunities, he should choose the one with the highest NPV.
A negative NPV would indicate that the investment doesn't meet investor expectations. A positive discounted cash flow indicates that the investment meets investor expectations.
The larger the net present value, the better the investment.

NPV Example 1					NPV Example 2
First period t = 1					First period t = 0
Discount Rate					Discount Rate
Initial Investment					Initial Investment
Annual Cash Flow					Annual Cash Flow

Year	Cash Flow	Discount Rate	PV	NPV	Year	Cash Flow	Discount Rate	PV	NPV
					0
1					1
2					2
3					3
4					4
5					5
6					6
7					7
8					8
9					9
10					10
note: -75,000 = -100,000 + 25,000 + first year Cash Flow calculation
					PV SUM		Year 10 (before Return of Ini. Inv.)
NPV		Year 10 PV Sum			NPV		Year 10 NPV plus Ini Inv.
IRR		Using Excel IRR Formula			IRR		Using Excel IRR Formula

NPV Examples

An investor is interested in an income-producing property. The NPV calculation would use the Initial Investment amount, a series of estimated yearly future after-tax Cash Flows, (the after-tax sales proceeds in a given year if the asset is sold) and a Discount Rate determined by the investor.

The income property requires an investment of $100,000, contributed at the beginning of the project. Cash Outflow (Expenses) for years 1 – 10 is expected to be $5,000 per year. Cash inflows (Income) are expected to be $30,000 per year for years 1 – 10. The Discount Rate determined by the investor is 10%. To determine the NPV, determine the present value (PV) for each year:

Note: This example does not have after-tax sales proceeds; download the Excel file associated with this example and you can make changes, including the addition of sales prodeeds to year 10 Cash Flow.

Example 1 - Using T = 1 for first period

Example 2 - Using T = 0 for first period

Member Posts

No posts exist.

Contribute to this page